- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本节课的授课对象是洪江区第二中学初三(3)班的学生,该班共有学生38人,数学成绩存在两极分化问题,一部分同学在课堂上能较为主动地完成相关学习任务,但思维不够活跃,对教师依赖性大;而其余大部分同学属于留守儿童,数学基础较差,缺乏良好的学习习惯,学习积极性不高;有个别学生甚至出现厌学情绪,对数学学习缺乏自信和动力,缺乏自制能力。因此,在教学过程中,应时刻关注学生的学习状况,根据学生接受情况及时调整教学策略,合理地设计分层练习,尽量使得不同层次地学生在学习中有不同地收获,逐渐增强学生对于学习数学的自信心。本课的前一节内容是点与圆的位置关系,由于内容简单,大部分学生掌握情况较好,能准确地通过比较点到圆心距离与半径的关系来判断点与圆的位置关系。因此本节课在设计导入时通过复习点与圆的位置关系,将“点”延伸到“线”,这样易于学生理解,符合几何认知规律。
多媒体白板交互系统、几何画板软件、PPT课件
【知识与技能】
1.理解、掌握直线与圆相交、相切、相离三种位置关系.
2.会根据圆心到直线的距离与半径的大小关系,或者公共点的个数来判断直线与圆的位置关系.
【过程与方法】
经历点与圆的位置关系过渡到直线与圆的位置关系的探索过程,让学生了解位置关系与数量关系的相互转化思想和数形结合思想,发展抽象思维能力.
【情感态度】
教学过程中让学生从不同的角度认识问题,采用不同的方法与知识解决问题,让学生在解决问题的过程中,学会自主观察与思考、讨论与交流,感受问题解法的多样性,思维的灵活性与合理性。
直线与圆三种位置关系及与之等价的数量关系
讲授法、直观演示法、任务驱动法、讨论法
同学们在海边看到过日出吗?请观察下面的图片,思考:我们能否用数学中的几何知识来解释日出的过程呢?

活动1:同一平面内,点与圆有哪几种位置关系?我们可以通过怎样的数量关系来判断?
学生思考后回答:
设⊙O的半径为r,点P到圆心距离OP=d,则有:
点P在⊙O外——d>r;
点P在⊙O上——d=r;
点P在⊙O内——d<r.
教师:如果将点变成直线,直线是否和圆还有类似的这样三种关系呢?这就是本课我们即将研究的内容。
探究一:直线与圆的三种位置关系
活动2:教师用几何画板展示直线与圆位置关系的变化动画,要求学生观察直线在平移过程中与圆公共点的个数.
在演示过程中,教师引导学生得到以下结论:
(一)当直线运动到下图位置时,直线l和圆有两个公共点,叫直线与圆相交,这条直线叫做圆的割线.
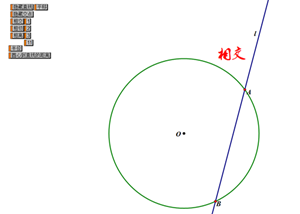
(二)当直线运动到下图位置时,直线l和圆只有一个公共点,叫直线与圆相切,这条直线叫圆的切线,这个点叫做切点.

(三)当直线运动到下图位置时,直线l和圆没有公共点,叫这条直线与圆相离.
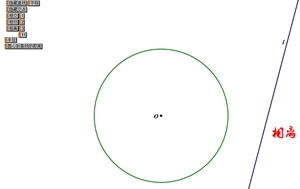
以上是从直线与圆的公共点的个数来说明直线和圆的位置关系的,还有其它更准确的方法(类比点与圆三种位置关系所对应的数量关系)来说明直线与圆的位置关系吗?
活动3:设⊙O半径为r,直线l到圆心O的距离为d,教师利用几何画板演示直线和圆的不同位置关系的切换过程,学生观察d与r之间的大小关系是如何变化?如何根据d和r的关系来确定直线与圆的位置关系呢?
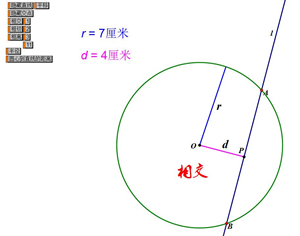
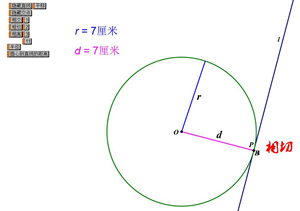
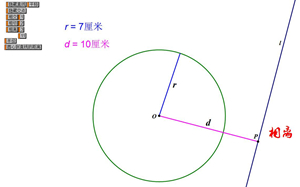
同学们观察,思考后分组讨论,由学生代表回答:
直线与⊙O相交——d<r
直线与⊙O相切——d=r
直线与⊙O相离——d>r
教师引导学生归纳:
这样,我们从“数”、“形”两方面得到了三种直线与圆的位置关系:
直线到圆心的距离d与半径r(数) | 公共点的个数(形) | 直线与圆的位置关系 |
d<r | 两个公共点 | 直线与⊙O相交 |
d=r | 一个公共点 | 直线与⊙O相切 |
d>r | 没有公共点 | 直线与⊙O相离 |
注:以上两种不同的角度来说明直线与圆的位置关系中,在今后的证明中以第一种居多.
例1(教材P65例1)
如图,∠C=30°,O为BC上一点,且CO=6cm,以O为圆心,r为半径的圆与直线CA有怎样的位置关系?为什么?
(1)r=2.5cm;
(2)r=3cm;
(3)r=5cm.
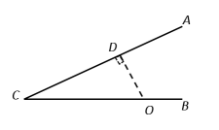
【分析】先根据题意计算出点O到AC边的距离d,再将r与d进行比较,得到相应的位置关系.
解:过O点做OD⊥CA交CA于D.
在Rt△CDO中,∠C=30°,
∴ OD=CO/2=3(cm).
即圆心O到直线CA的距离d=3cm.
(1)当时r=2.5cm,有d>r,因此☉O与直线CA相离;
(2)当时r=3cm,有d=r,因此☉O与直线CA相切;
(3)当时r=5cm,有d<r,因此☉O与直线CA相交.
例2 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4. 若以点C为圆心,r为半径的圆与斜边AB只有一个公共点,求r的取值范围?
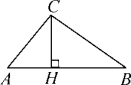
【分析】此题中以r为半径的圆与斜边AB只有一个公共点,此时要注意相切和相交两种情形,由于相交有两个交点但受线段AB的限制,也有可能只有一个交点,用几何画板演示后让学生自主解答,需提示学生在几个关键点的取舍.
解:∵∠C=90°,AC=3,BC=4,∴CH=5
又∵△AHC∽△ACB,∴AC:AB=CH:BC ,即3:5=CH:4,CH=2.4
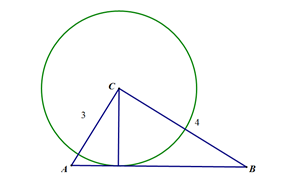
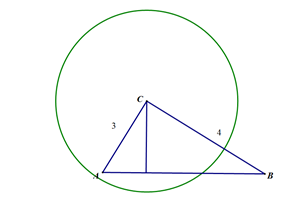
(1)当r=2.4时,☉C与边AB相切,有一个公共点;
(2)当3<r≤4时,☉C与边AB相交但只有一个公共点.
【教学说明】要判断直线与圆的位置关系,关键是找出圆心到直线的距离d,再与圆的半径进行比较,要熟练掌握三个对应等式.
1.已知⊙O的半径为5,圆心O到直线l的距离为3,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
【分析】直接比较圆心到直线距离与半径间的数量关系.距离小于半径,因此选A.
2.设⊙O的半径为3,点O到直线l的距离为d,若直线l与⊙O只有一个公共点,则d应满足的条件是( )
A.d=3 B.d≤3 C.d<3 D.d>3
【分析】由只有一个公共点得知距离等于半径,因此选A.
3.已知⊙O的直径为6,P为直线l上一点,OP=3,则直线l与⊙O的位置关系是_____ .
【分析】需要分两种情况讨论:OP⊥l时,相切;OP与直线l不垂直时,相交。
4.在Rt△ABC中,∠C=90°,AB=4cm,BC=2cm,以C为圆心,r为半径作圆. 若直线AB与⊙C:(1)相交,则r____;(2)相切,则r____;(3)相离,则____<r<_____.
【分析】需按题意画出图形,求出斜边上的高,即为点C到AB边的距离d,再根据直线与圆的位置关系来判断r与d的数量关系.
5.如图,已知Rt△ABC的斜边AB=8cm,AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB所在直线与⊙C相切?
(2)以点C为圆心,分别以2cm和4cm为半径作两个圆,这两个圆与AB所在直线分别有怎样的位置关系?
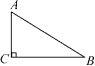
【分析】与上题类似,需先求出AB边上的高,即为点C到AB的距离.
1.这节课你学到了什么?还有哪些疑惑?
2.在学生回答基础上,教师强调:
①直线和圆相交、割线、直线和圆相切、切点、直线和圆相离等概念.
②设⊙O半径为r,直线l到圆心O的距离为d,则有:
直线l与⊙O相交d<r
直线l与⊙O相切d=r
直线l与⊙O相离d>r
1.教材P65练习第1、2题.
2.完成同步练习册中本课时的练习.(选做)
设为正确答案